We are asked to find an element in a sorted array of n integers that has been rotated an unknown number of times, and to find it in O(log n). We are told the array was originally sorted in increasing order. Much like you see below. 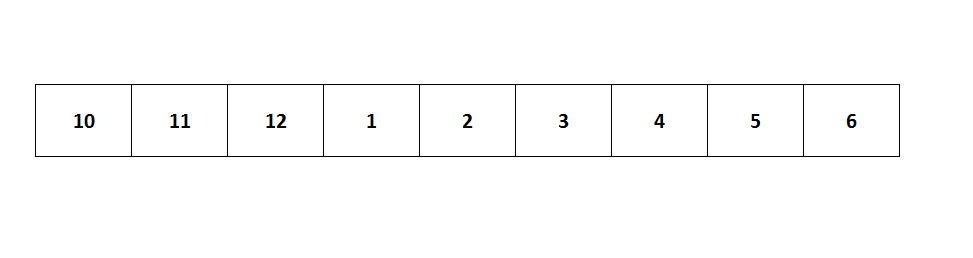If you look at that O(log n) requirement and think, must be binary search, then you are correct. Though, with a little twist. Since our array is not in increasing order from 0 → n, we have to figure out where we can apply the binary search.

Step through a simple example on paper, put the text editor away for now. We see that in the image above binary search applies for elements 3 → end. So how do we search the array for that starting point and still run in O(log n). Just need to tweak the typical binary search.

We will jump through the array by half still, but instead of comparing with the number you are searching for, we will compare the number with the next number in the array. All the while, we must keep track of the starting index. Otherwise, we will not know where we are in the array when we’re splitting the array in our searches. Here is what it looks like in JavaScript.

function rotated_sorted_array_search(arr, num){
  var index = 0;
  var half = Math.floor(arr.length / 2); // no float indexes
  while(arr[0] > num){
    if (arr[half] === num){
      arr = arr.slice(half);
      index += half;
      break;
    }
    if (arr[half] > num){
      if(arr[half] > arr[half + 1]){
        index += half;
        arr = arr.slice(half);
        half = Math.floor(arr.length / 2);
      }
      else{
        arr = arr.slice(0, half);
        half = Math.floor(arr.length / 2);
      }
    }
    else {
      index += half;
      arr = arr.slice(half);
    }
  }
...
}

We will loop while the first element of the array is still greater than the number we are searching for. Every iteration we will cut the array in half. The index is only increased when we are taking only the second half of the array. Each iteration will continue to cut it until we end up with an array where the first element is <= to the number we are searching for. Makes sense right. We can’t apply binary search to an array until it becomes completely sorted from beginning to end.

Now we have an array that we can apply binary search to. Once we call binary search we are basically donezo. The index must be passed into the binary search once again and incremented in the same fashion as above. Here is the rest of the snippet to complete the function. First the binary search function that accounts for the index is made.

function binSearch(arr, num, idx){
    var half = Math.floor(arr.length/2);
    if (arr.length === 1 ){
      return idx;
    }
    else if (arr[half] > num) {
      idx = binSearch(arr.slice(0, half), num, idx);
    }
    else{
      idx += half;
      idx = binSearch(arr.slice(half), num, idx);
    }
    return idx;
}

Now that we have a functioning binary search, we can call it on the sorted array we created above. The final solution will look like the following.

function rotated_sorted_array_search(arr, num){
  var index = 0;
  var half = Math.floor(arr.length / 2);
  // find part of array that contains the num searched for
  while(arr[0] > num){
    if (arr[half] === num){
      arr = arr.slice(half);
      index += half;
      break;
    }
    if (arr[half] > num){
      if(arr[half] > arr[half + 1]){
        index += half;
        arr = arr.slice(half);
        half = Math.floor(arr.length / 2);
      }
      else{
        arr = arr.slice(0, half);
        half = Math.floor(arr.length / 2);
      }
    }
    else {
      index += half;
      arr = arr.slice(half);
    }
  }
  // binary search for index of num
  index = binSearch(arr, num, index);
  return index;
}

Disclaimer: I am aware that this can be done in fewer lines and not having to build a separate binary search function. I did so for to make it more explicit for someone who is approaching this problem for the first time.

Cheers